Nitijou Analysisのカテゴリーでは、
日常生活で何となく思っていたことをそれっぽい形に考察してみることで、
宇宙の真理を解き明かすことを目標としています。
ですがいきなり真理の探究は荷が重いので、「先ず$\chi$より始めよ」ということわざもあることですし、
日常生活の中からできるアプローチを行っていきます。
今回の目次です。あんまりいらないかも。
はじめに
皆さん、車や電車に乗ったことはありますか?
たわんだ電線を車窓から見ていると、「円弧だなぁ」と感じますよね。
マエストロになればコーナーで体力が回復したりする、あの円弧です。
なんか、あの、上手く表現できないけど雲のイラストの下半分みたいな感じあるんですよね。

拝啓
サンタさんへ
クリスマスプレゼントは語彙力をお願いします。
ぼく
敬具
あるいはクラブにいる縦ノリの人間の頭の動きでしょうか。
乗り物の速度によってBPMが変わっているように見えるのでそれはそれで面白い。
電車のような速い乗り物であればBPM200近くになりそうですね?ブチ上がりすぎてるだろ。
人生で一回はこれを計算しておかなければならないという使命感が湧いてきたので、やります。
ですが電線の懸垂曲線(カテナリー)を真面目に計算するのはめんd…複雑な数式が必要なので
概算で行おうと思います。フェルミ推定ってやつですね。(言いたいだけ)
フェルミ推定
実際に調査するのが難しい数値を、いくつかの手がかりを元に論理的に推論し、短時間で概算すること。
例えば、「シカゴにピアノ調律師は何人いるか?」みたいな、
ググっても一発で出ない答えを、手持ちの知識と妄想力で無理やり推定しようとすることです。
大味であればあるほど面白いとされている。(当社比)
なあフェルミ、なんで俺は貯金ができねぇのか教えてくれよ。
懸垂曲線(カテナリー)
重力に身を任せたロープが描く、だらけた曲線。見た目は放物線に似てるけど、実は別物。
俺のモチベーションもこれ。だったらよかったのになぁ。
でbest fitされてしまっている。
計算方法:うーん、全部目測!w
まず、「見ている電線は、巨大な円の一部を切り取ったものである」とします。
使う道具は、中学校の数学の授業中に居眠りしていなければ覚えているはずの
「三平方の定理(ピタゴラスの定理)」だけ。 カテナリーの微分方程式? 誰?
具体的な手順はこうです。
- 電柱と電柱の間隔(幅)を目分量で測る(これをとします)。
- 電線の垂れ具合(深さ)を目分量で測る(これをとします)。
- この2つの数字から、円の半径 を逆算する。
図にすると、電線の最下点から「円の中心」に向かって直角三角形が作れます。
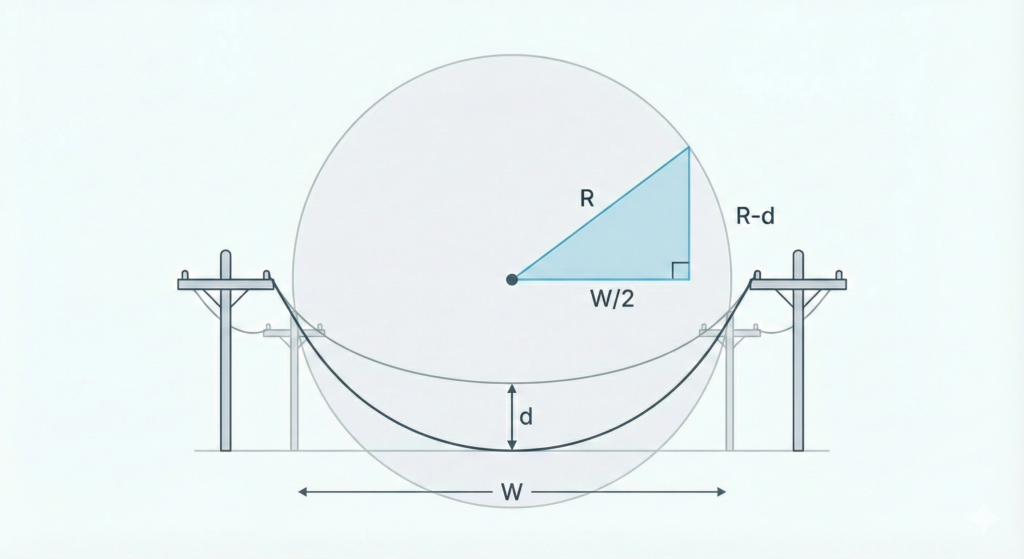
それにしてもAIって便利ですねぇ~
ここで、三平方の定理を召喚(サモン)します。試験召喚獣ではありません。
余談なんですが、皆さんは「三平方の定理」派ですか?「ピタゴラスの定理」派ですか?
個人的には「きのこ/たけのこ論争」に匹敵するレベルの派閥争いだと思っています。
図に適応すると
これを「半径 について解け」という数学ドリルみたいな展開になりますが、展開して整理するとこうなります。
下付き文字付けるの面倒なので省略しました。
電線のたわみは、電柱間の幅 に比べてめちゃくちゃ小さいので、
なんて誤差なんだよ、誤差!無視します。
「細かいことは気にするな」、私の好きな言葉です。
すると、驚くほどシンプルな式が爆誕します。
つまり、「電柱間の距離 () を2乗して、たわみ () の8倍で割る」だけで、あの巨大な円弧の半径が出せるのです。
分母に8がいるのが少し気に食わないですが、まあ許容範囲でしょう。
これで、車窓から流れる電線を見るだけで、電線のカテナリーが作る円の半径が推定できるようになります。
勿論、dが小さいほど、Rは2乗に比例して大きくなります。
じゃあ計算、しちゃいますか(暗黒微笑)
瀬戸大橋線で計算してみよう
今回は四国から我が祖国、大都会岡山へ続く大動脈である、瀬戸大橋線で概算します。
他の路線も計算するのがめんどくさいとかいうわけではありません。決して。
この路線の目玉はなんといっても
征外大橋(かつて死国を平定する際に使用された職人の血と汗の結晶である世界に冠たる鉄道道路併用橋)
です。
鉄オタの知識を勝手に拝借して、橋内のを30mと仮定します。
たわみは目測で0.5mとします。
と半径225mの円であることが分かります。
では当然面積は
長いので、としましょうか。最後のゆとり教育世代ですが、3とはしません。
そうすると、
(約16万平方メートル)
となります。
これは…何で例えましょう?
よく東京ドーム何個分かで大きさを表現しますが、
地方民の僕からしたら「東京ドーム?なんすかそれ笑笑」でしかないので、
より普遍的な例を探しました。
Ⅰ.後楽園
言わずと知れた、後楽園です。
中四国最大の都市圏である岡山都市圏の中核、岡山市の一等地に悠然と佇む岡山城の庭園です。
総面積は約133,000m²。
車窓から見える送電線が作る円は、この広大な後楽園を余裕で収まるサイズの巨大な円だったわけです。
そう考えると結構面白いな。
やはり岡山は西日本の盟主になるべき存在です。
中四国の二番手ポジションで満足してんなよ!!!!!!!!!!!!!!!!!!!!!!!!!
岡山市は何をやってるんだ!
まず、広大で盤石な土地と圧倒的なアクセスを生かして巨大なデータセンター群や、
国家機能・大企業の第二本社を誘致して「日本のバックアップ」としての地位を確立してだな……
失礼。皆さんも瀬戸大橋線に乗る機会があれば、車窓を眺めながら後楽園を想像してみてください。
Ⅱ.城山公園(堀之内地区)
松山市の中心にどっしりと構える松山城の麓に広がる長閑で自然豊かな美しい公園です。
平地部分の面積は全体で約16〜17万m²です。
今回の計算結果とかなり近いですね。
松山市民の皆様、松山城の方角を向いてください。
あの「やすらぎ広場」を含むお堀の中のエリア全体。あれが、電線のビヨンビヨンしたカーブが描く円の大きさです。
城山公園と言ったら……ほろよいフェスタですよねぇ!!!!!!!!!!!!!!!!111!!!!!!!11!!!!
入場料払ったら指定席でプラスチックのシャンパングラスみたいなん渡されて意味わからんほど日本酒飲みまくれるアレです。
おっちゃんに「ストップ言(い)うてね~」って言われながら
日本酒を意味不明なくらい注がれるイベントなんてほろよいフェスタ以外聞いたことありません。
例年十月頭に開催されます。入場料は僕が行ったときは6000円でした。
一度入ったら愛媛の地酒が30種類以上飲み放題です。時間制限は特にありませんが、閉会するまで4時間くらいあった気がします。
周りに愛媛のB級グルメの出店もあってマジの神環境なので、これ目的で愛媛に来てもいいくらいです。
(入場料が高いので参加客の治安がいい。大人の出会いの場みたいになっているのでソロはあまりお勧めしませんが。)
地酒が美味しすぎるので飲みすぎに注意(一敗)。
最後にもう一つ
最後に、世界で一番長い送電線で計算してみましょうか。
世界で一番長い送電線はGemini君によると
グリーンランドにある「アメラリック・スパン(Ameralik Span)」というやつらしいです。
鉄塔と鉄塔の間隔が「5,376メートル」あるらしい。この距離で海底ケーブルじゃなんだ。脳筋すぎる。
たわみですが、 これだけの長距離だと、自重で相当たわみます。
あまりピンと張ると張力で切れてしまうため、あえて深くたわませているはずです。
一般的に、長大スパンのたわみ率(サグ・レシオ)は数%〜10%近く取ることがあります。
ここは大胆に、幅の約5%ほど垂れ下がっていると仮定しましょう。
とします。 なが。
では計算してみると
となります。
え、?
これくらいデカいと、
約627 km²であるほぼ「東京23区」がまるごと入る円です。 (世田谷区や大田区がちょっとはみ出るくらい)
おもろ。
淡路島(約592 km²)はすっぽり入ります。
はえ~、デカすぎんか?
グリーンランドのフィヨルドで風に揺れる電線を見つめることは、 「空に浮かぶ淡路島」を見つめることと同義だと言えます。
流石にラピ〇タやドラ〇エⅨの天使界くらいのは存在しないか……
これが現実の限界なんですね。悔しい。
なんか余談の割合がデカい気がしますが、別に大きさってそんな言うことなくないですか?
〇〇くらいなんですよ~ へぇ~
で、終わりじゃない?????????????????????????????????
とはいえ、へぇ~となるのは楽しいので問題ありませんが。
さいごに
どうでした?
日常でふと思ったことを実際に計算してみることって結構面白いですね。
本当はもっといろいろな路線で計算してみたかったのですが、気力の限界です。
無限のモチベーションが欲しいよ~~~~~~~~~~~
また何か「これ計算できるんじゃね?」ってやつを見つけたらガバガバ試算をやってみます。
こんなんに正確性を求めるのはナンセンスですからね。
空想科学読本ならもうちょっと真剣に計算していると思います。
そう考えるとすごいっすね、あの本。今回で実感しました。
ではまた。





コメントを残す